Santiago's blog

Why Are Kronecker Products So Effective?

02 Apr 2021 - Raúl Santiago Molina

A few days ago, the list of ICLR 2021’s Outstading Paper Awards was announced. One paper immediately caught my attention from the list: Beyond Fully-Connected Layers with Quaternions: Parameterization of Hypercomplex Multiplications with \(1/n\) Parameters.

The main contribution of the paper is the “parameterized hypercomplex multiplication (PHM) layer”, a new layer that can replace fully connected (FC) layers with high parameter efficiency.

The PHM Layer

Instead of having a normal FC layer like this:

\[\bf{y} = FC(\bf{x}) = \bf{W}x + b\]

We would have a PHM layer:

\[\bf{y} = PHM(\bf{x}) = \bf{H}x + b\]

For both layers we are learning a linear mapping (\(\bf{W}\) or \(\bf{H} \in \mathbb{R}^{k \times d}\)) of the input \(\bf{x}\).

To have a clear understanding of what the proposed layer does, the authors introduce the Kronecker Product. For matrices \(\bf{A} \in \mathbb{R}^{m \times n}\) and \(\bf{B} \in \mathbb{R}^{p \times q}\), the Kronecker Product \(\otimes\) is defined as:

\[\begin{align*} \bf{A} \otimes \bf{B} = \begin{bmatrix} a_{11}\bf{B} & \dots & a_{1n}\bf{B} \\ \vdots & \ddots & \vdots \\ a_{m1}\bf{B} & \dots & a_{mn}\bf{B} \end{bmatrix} \in \mathbb{R}^{mp \times nq} \end{align*}\]

The end result of applying the Kronecker Product to two matrices, is another matrix (a block matrix). With the assumption that both dimensions \(k\) and \(d\) are divisible by a user-selected positive integer \(n\), the matrix \(\bf{H}\) from the PHM layer can now be defined:

\[\begin{align} \bf{H} = \sum_{i=1}^n \bf{A_i} \otimes \bf{S_i} \end{align}\]

Where \(\bf{A_i} \in \mathbb{R}^{n \times n}\) and \(\bf{S_i} \in \mathbb{R}^{\frac{k}{n} \times \frac{d}{n}}\).

Such construction makes \(\bf{H}\) very efficient in terms of parameter count, with approximately \(1/n\) the number of parameters of an FC layer matrix \(\bf{W}\). Assuming that \(kd > n^4\), which is the case for high dimensional latent spaces found in practice.

One of the first things I questioned after seeing this equation was the restriction of \(\bf{A_i}\) to be a square matrix. The authors provide an intuitive explanation from the point of view of quaternion multiplication (hence the name “hypercomplex multiplication”, as the quaternion number system is a kind of hypercomplex number system). A nice property of quaternion multiplication (called the Hamilton Product), is that it can be rewritten as the following matrix:

\[\begin{align} \begin{bmatrix} Q_r & -Q_x & -Q_y & -Q_z \\ Q_x & Q_r & -Q_z & Q_y \\ Q_y & Q_z & Q_r & -Q_x \\ Q_z & -Q_y & Q_x & Q_r \\ \end{bmatrix} \begin{bmatrix} P_r \\ P_x\\ P_y\\ P_z \\ \end{bmatrix}, \end{align}\]

Where each subscript is associated with the quaternion unit basis.

This matrix can be interpreted as defining a rotation \(Q\) of a 3-Dimensional vector \(P\), which is very useful as an inductive bias to learn rotations inside Neural Networks (an experiment demonstrated in the paper). However, in its common form is not very useful for other dimensions, so the authors propose to reformulate it as the sum of Kronecker Products:

$$ \begin{align} \label{eq:ASQ_kron} \underbrace{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} }_{\bf{A_1}} \otimes \underbrace{ \begin{bmatrix} Q_r \\ \end{bmatrix} }_{\bf{S_1}} + \underbrace{ \begin{bmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} }_{\bf{A_2}} \otimes \underbrace{ \begin{bmatrix} Q_x \\ \end{bmatrix} }_{\bf{S_2}} + \underbrace{ \begin{bmatrix} 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ \end{bmatrix} }_{\bf{A_3}} \otimes \underbrace{ \begin{bmatrix} Q_y \\ \end{bmatrix} }_{\bf{S_3}} + \underbrace{ \begin{bmatrix} 0 & 0 & 0 & -1 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix} }_{\bf{A_4}} \otimes \underbrace{ \begin{bmatrix} Q_z \\ \end{bmatrix} }_{\bf{S_4}} . \end{align} $$

As can be seen, the matrices \(\bf{A_i} \in \mathbb{R}^{4 \times 4}\) and \(\bf{S_i} \in \mathbb{R}^{\frac{4}{4} \times \frac{4}{4}}\), which demonstrates that a PHM layer with \(n=4\) can learn quaternion multiplication. Given that the same result holds for \(8D\) (octonions), \(16D\) (sedenions), and the fact that \(n\) can take more values than just \(\{4, 8, 16\}\), the PHM is said to generalize hypercomplex multiplication to \(nD\).

To close this section about the PHM layer, I want to show the results they achieved applying the layer to machine translation, which offers great results in parameter efficiency without sacrificing much performance:

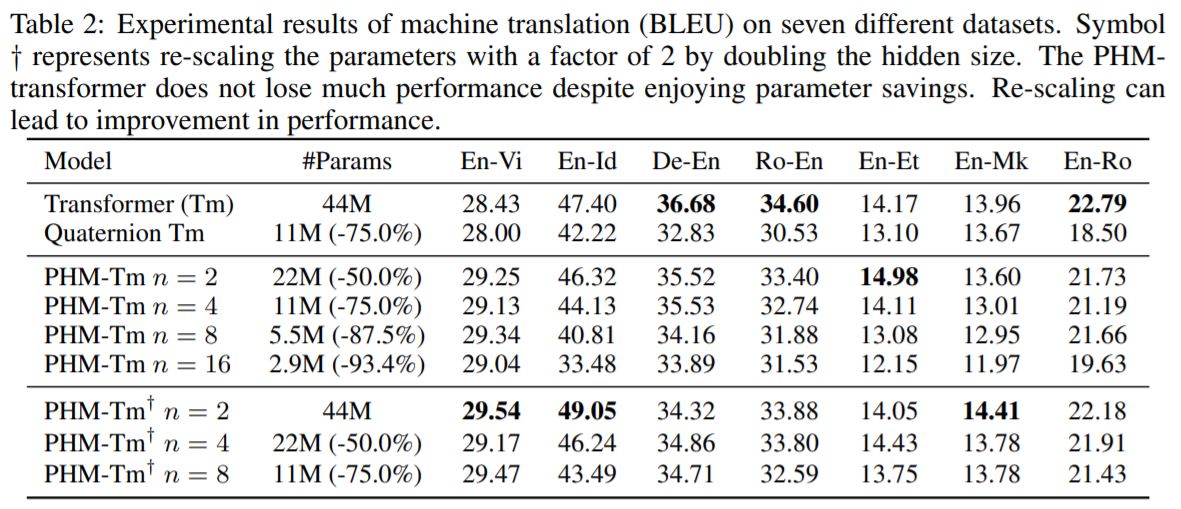
Why are Kronecker Products effective then?

This paper caught my attention because I had read about the Kronecker Product being used in a similar manner for Convolutional Neural Networks. In particular, a 2015 paper called Exploiting Local Structures with the Kronecker Layer in Convolutional Networks.

In this paper two new types of layers are proposed. First the Kronecker Fully-Connected (KFC) layer:

\[\begin{align} \mathbf{L_{i+1}} = f\left(\left(\sum_{i=1}^{r} \bf{A_i} \otimes \bf{B_i}\right)\bf{L_i} + \bf{b}_i\right), \end{align}\]

where \(\bf{A_i} \in \mathbb{R}^{m_1^{(i)}\times n_1^{(i)}}\), \(\bf{B_i}^{(i)} \in \mathbb{R}^{m_2^{(i)}\times n_2^{(i)}}\), \(m_1^{(i)}m_2^{(i)}=m, n_1^{(i)}n_2^{(i)}=n\) and \(r \in \mathbb{N^+}\).

And its generalization the Kronecker Convolutional (KConv) layer:

\[\begin{align} \mathcal{W} \approx \sum_{i=1}^{r}\mathcal{A}_i\otimes\mathcal{B}_i, \end{align}\]

where \(\mathcal{A}_i\) and \(\mathcal{B}_i^{(i)}\) are \(4D\) tensors with similar shape constraints as the cases before.

In contrast to PHM, the authors of the KConv paper arrive to the sum of Kronecker Products not by construction, but by improving on the ideas about low rank decomposition of Convolutional Neural Networks proposed in Speeding up convolutional Neural Networks with low rank expansions and Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation, amongst others.

Particular emphasis must be made on their use of the duality between approximating weight matrices using the sum of Kronecker Products and Singular Value Decomposition (SVD). This duality is demonstrated in Section 5.5 of the paper Approximation with Kronecker Products, and it is crucial, as it gives a hint on why such parametrizations work in practice:

“Next, we consider the situation when the matrix A to be approximated is a sum of Kronecker products:

\[A=\sum_{i=1}^{p}\left(G_{i} \otimes F_{i}\right) .\]

Assume that each \(G_i \in \mathbb{R}^{m1 \times n1}\) and each \(F_i\in \mathbb{R}^{m2 \times n2}\). It follows that if \(f_i = vec(Fi)\) and \(g_i = vec(G_i)\), then:

\[\tilde{A}=\mathcal{R}(A)=\sum_{i=1}^{p} \mathcal{R}\left(G_{i} \otimes F_{i}\right)=\sum_{i=1}^{p} g_{i} f_{i}^{T}\]

is a rank-\(p\) matrix.”

Although explaining the rearrangement operation \(\mathcal{R}(A)\) is beyond the scope of this post (I highly encourage you to read the paper). This result shows how solving the problem of approximating a matrix \(A\) with the sum of \(p\) Kronecker Products is equivalent to the rank-\(p\) SVD of a rearranged version of \(A\).

As it is the case with many signals in the real world, the intrinsic dimensionality of the transformer weights in the PHM paper is likely to be small. As such, low-rank approximations might be able to capture most of the model behavior with few parameters, explaining the efficiency of the Kronecker Product approach.

Final thoughts

I came across the Kronecker Product back in 2018, when I worked on a school presentation about incorporating large scale context in Neural Networks. Although I started by looking at what was novel at the time (Deformable CNNs and the Atrous Spatial Pyramid Pooling scheme in Deeplab), it wasn’t until I found a great blog post by Ferenc Huszár outlining the relationship between Dilated Convolutions and Kronecker Factored Convolutions that I became captivated by the subject.

As it turns out, there has been a long chain of papers on making Neural Networks efficient, all with different takes on which is the best way to do Matrix (or Tensor) Decomposition. From the ideas that influenced the development of the KConv layers to the novel connection with hypercomplex multiplication proposed with the PHM layer, I have become convinced that the Kronecker Product will be a crucial tool in the path to understanding Neural Networks.

References